i got a question...uh...hehe....are we supposed to add to our original growing post, cause thats waht ive been doing..or do we make a whole new post, cause thats what evryone else is doin......
cause right now i have all the 3 growing posts on my original one......sorry for the inconvience :-/
-michael
posted by apuya_soldier_ @ 5:19 p.m.
2 comments
Week of Sunday, May 7, 2006, to Saturday, May 13, 2006
#1: What is meant by the terms "Rotation Symmetry" and "Reflection Symmetry"? How does this relate to pentominoes? Explain these terms so that anyone who reads your post understands what you mean.
Rotation symmetry is symmetry with respect to rotations, like isometries that preserve orientation. For instance, you can take any point on any shape, and rotate on the point, and it'll still be the same shape, thus preserving the orientation.
Reflection symmetry is symmetry with respect to reflection, and is the most common type of symmetry. It consists of a "axis of symmetry" which is an imaginary line that if you put a perpendular, any 2 points on that perpendicular on opposite sides of equal distances from the axis of symmetry are exactly the same.
These two terms relate to pentominoes because you can rotate (like in rotational symmetry) and flip (like in refectional symmetry) them.
#2 Create a pattern. You must represent this pattern both pictorially (i.e. with a picture or diagram) and with numbers. You must show the first 4 steps of your pattern.
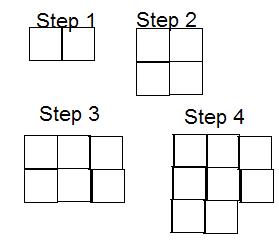
#3: Describe in words what is occuring with your pattern and if your pattern has an ending or if it continues on indefinately. Make sure that your explanation is clear enough that the person reading your description could understand your pattern without seeing your diagram.
In this very crude-made pattern, it starts as a rectangle that consists of two squares, horizontally.
Then in the next step, it adds another rectangle made of two squares to the bottom horizontally, making a square made of four smaller squares.
In the third step, it does a similar thing by adding another two-square rectangle only it's on the right of the shape, and is vertical, creating a six-square rectangle horizontally, with two rows and three columns.
And in the fourth shape it adds yet another two-square rectangle on the bottom this time, horizontally, aligned to the left side of the shape, creating a shape close to that of a square with nine smaller squares, only with a square missing at the bottom-right corner of it.
This pattern is able to go on forever and ever, ultimately creating a long upside-down, flipped-horizonally letter L.
#4: Create a T-Chart that shows what is happening with your pattern. You must show the first 4 steps of your pattern with the T-chart.
- michael
Week Of Sunday, May 14, 2006 To Saturday, May 21, 2006
Question #1: Solve all 3 parts of the problem below
Jack collects baseball cards. Jack has 180 baseball cards in his collection. At the end of each month Jack buys 25 baseball cards to add to his collection.
a)Create a T-Chart showing how many baseball cards Jack has at the end of the next 4 months.
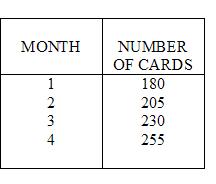
b)Create an algebraic formula based upon the problem above
(n=month)
185+25(n)
c)If Jack just turned 8 years old this month and Jack continues to buy the same amount of baseball cards each month, how many baseball cards will jack have when he turns 12?
He will have 1385 cards when he's 12
Question #2: Use the chart to figure out the questions below.
Jackie is planning on having a pizza party with some of her friends. She is trying to figure out how many pizza’s to order. She knows that each pizza has six slices of pizza.
a)If Jackie thinks that there will be four people at the party (counting herself) how many pizza’s should she order?
She should order 2 pizzas.
b)If two more people show up at the party how many more pizza’s does she need to order?
She should order 3 pizzas.
Question #3: Answer the questions below based upon this information
Kathy has $20 in her savings account. Each month she adds another $15 to her savings account. In order to calculate how much money she will have in one year Kathy has created this algebraic formula: 20 + 15n = Savings amount
a) Calculate how much money Kathy will have in one year
She'll have $200 in one year
b) Suppose Kathy counted wrong and she really has $25 in her account instead of $20. Change the algebraic formula to reflect this miscalculation.
25+15n= savings amount
Question #4: Solve the following equations. Show all of the steps that are needed.
a) 3n + 4n + 7 = 2n + 12 ---> 12n + 7 = 2n + 12 ---> 12n - 2n + 7 = 2n - 2n + 12 ---> 10n + 7 = 12 ---> n=0.5
b) 8n – (4 + 9) = 11 ---> 8n - 13 = 11 ---> n=24
c) (8 – 3 )n + 7n + 8 = 4n + 40 ---> 5n + 7n + 8 = 4n + 40 ---> 12n + 8 = 4n + 40 ---> 12n - 4n + 8 = 4n - 4n + 40 ---> 8n + 8 = 40 ---> n=4
Question #1: What is the difference between an algebraic expression and an equation (hint: one contains this and the other doesn't)? Give an example of both an expression and an equation.
An equation already has the value of the varible(s) given, while in an expression, the value of the variable(s) can be chosen.
An equation is something like: 4+2n=12.
An expession is something like: 4+2n=.
Question #2: What is a variable and why do we use one in algebra?
A variable is a number with an unkown value that has the potential to change, and can be in an expression or an equation.
Question #3: Solve for N
N is equal to 11, because...
a square is equal to 2, a circle is equal to 1, and since a picture of 2 squares and a triangle is equal to 9 circles, we can say that because 2 squares is 4 and leaves 5, a triangle is equal to 5.
and since 2 "N"s are equal to 6 squares and 2 triangles (6 squares+2 triangles=22, and 22/2=11), N is equal to 11.
Question #4: Solve the following equations. Show all the steps that are needed.
A) 3n+4n+7=2n+12 ---> 7n+7=2n+12 ---> 7n=2n+5 ---> 5n=5 ---> n=1
B) 8n-(4+9)=11 ---> 8n-13=11 ---> 8n=24 ---> n=3
C) (8-3)n+7n+8=4n+40 ---> 5n+7n+8=4n+40 ---> 12n+8=4n+40 ---> 12n=4n+32 ---> 8n=32 ---> n=4
Question #5: For this question you need to create a T-chart and a graph to plot your data onto.
You are having a race against your friend, except you are on foot and he is on his bike. You both know that if you are on your bike, you will be faster so your friend gives you a head start of 3 minutes. If you can run 400m per minute, and your friend can bike 700 per minute, who will be the first to make to the finish line 2000m away?
Question #1: Formulas
Sentence 1: 13x=2 converted to....11+2=Scotts age, which is 13...(since this was easy, i think i did something wrong, pls tell me mr reece!)
Sentence 2: we can say that she makes $80 a month... 200x+b=80 (b=months) converted: 200+80n= (n=months) so in this case...200+80(12)=1160...so she'll have a whopping $1160 after one year.
Question #2: Creation
My Question and Answer 1: Solve for n:
3n-7+9=14.... to solve this problem...
3n-7+9=14--->3n-7+7+9-9=14--->3n=12--->(since 12/3=4)n=4
My Question and Answer 2: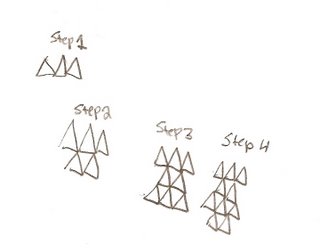
What will be the next 2 steps in the pattern, and create a t-chart for the first 6 steps.
Question #3: Reflection
A topic that I colored red or yellow is "Can I create a t-chart for my pattern?". I have learned more easier ways to transfer data between t-charts, graphs, and equations, as now I know that the "x" value should be on the left of the chart and opposite for the "y" value.
Question #4: Preparing For The Final Exam
I think that I have done well this year in all topics but I think my weakest topic is....the measurement of area of an irregular shape because I need more practice on doing this. Like for instance...
in thi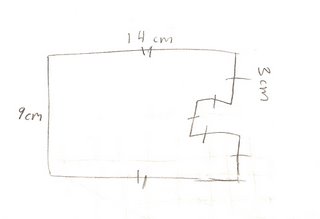
s photo, i would make those two 3x3 squares their own shape, but on the 14cm part, i woulden't subtract 3 from the calculations.
posted by apuya_soldier_ @ 5:37 p.m.
4 comments
If you can't remember what is required for the growing post assignment click here to go to the post on my blog.
posted by Mr. Reece @ 7:46 a.m.
0 comments
A box contains two coins. One coin is heads on both sides and the other is heads on one side and tails on the other. One coin is selected from the box at random and the face of one side is observed. If the face is heads what is the probability that the other side is heads?
i got this here.
- michael
posted by apuya_soldier_ @ 6:36 p.m.
0 comments
